Bak-Tang-Wiesenfeld Model for Displaying Self-Organized Criticality.
aka Abelian Sandpile Model, written in Python using the Matplotlib module.
Spring 2012:
CSCI 577 - Computer Simulation and Modeling - Dr. Jesse Johnson
"Who could ever calculate the path of a molecule? How do we know that the creations of worlds are not determined by falling grains of sand?" - Victor Huge, Les Miserables.
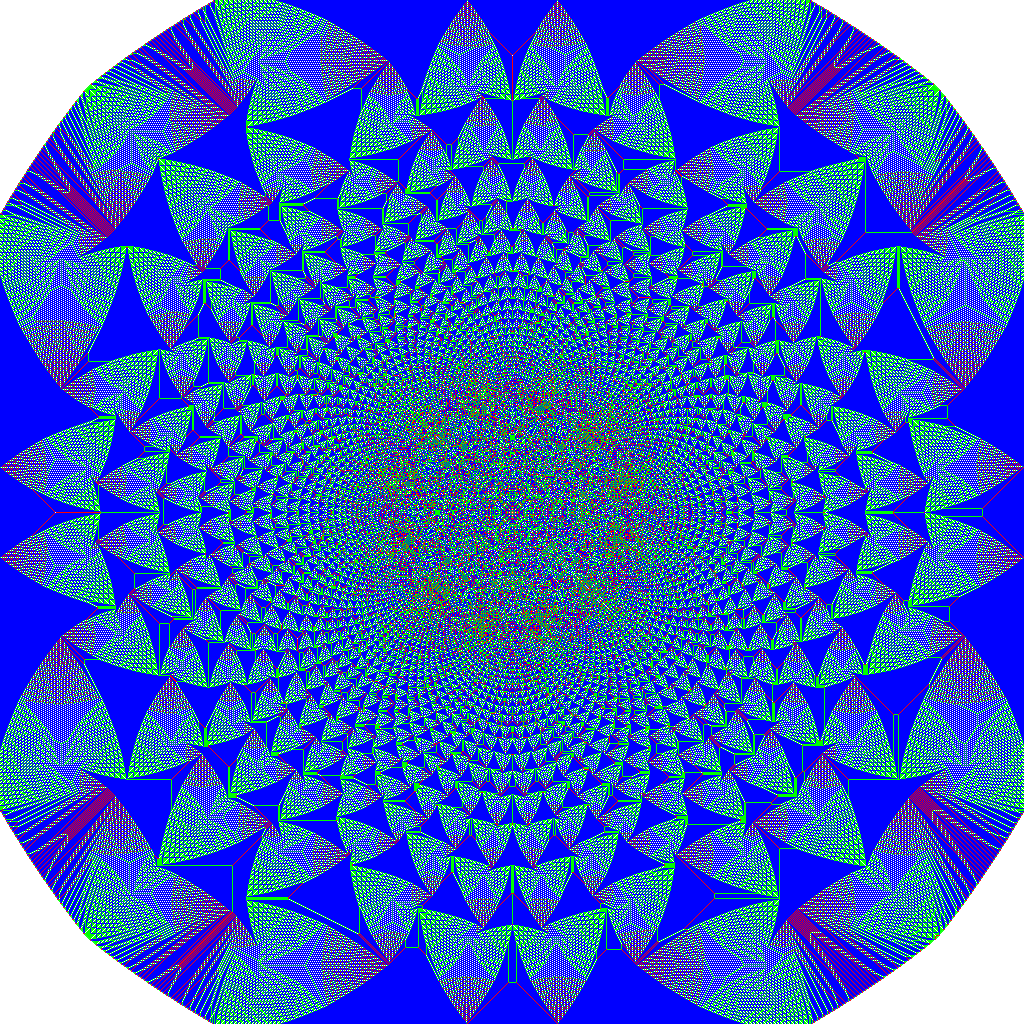
28 Million Grains of Sand Dropped.
What was the project assignment?
The project assignment was to read a paper that discussed a particular biological system and create a computer model and simulation for that system. I chose the Bak-Tang-Wiesenfeld Model
for Self-Organized Criticality, which is discussed in the Physical Review Letters
journal article Volume 59, Number 4 (July 27th, 1987) and in great
detail in their 1996 publication, How Nature Works. Here are theWeb Review and Amazon
pages if you are interested in this system in greater detail.
The premise of theBak-Tang-Wiesenfeld sandpile modelis that there are some grains of sand being dribbled from some higher place (i.e., someone pouring sand through a funnel or dropping sand
from their hand) onto some lower place that becomes a pile of sand. The sand lands randomly on the sandpile and slowly builds up the sandpile's slope in different places.
Eventually, the slope reaches some point of criticality (called theAngle of Repose) and avalanches downward, affecting
all the sand grains below. Sometimes, this results in a large domino effect of avalanches, but sometimes this means only one small pile will topple. Per Bak showed
that this behavior happened in patterns and followed a power ratio referred to asPink Noise or 1/f noise.
Basically, this meant that the larger the avalanche or catastrophe, the less frequent this event would occur. They found that these avalanches created a phenomena, which Per
Bak noted followed the theory ofSelf-Organized Criticality. This self-organized criticality was responsible
for volcano eruptions, earthquakes, mountain and galaxy formation, as well asNeural Activity, according to Bak.
How Nature Works claims that this 1/f noise could be seen throughout the measurable universe.
My job was to demonstrate that this was true on a small scale with a computer simulation of this model. I did so by writing a cellular automata in Python, using theEnthought Python Distributionlibraries
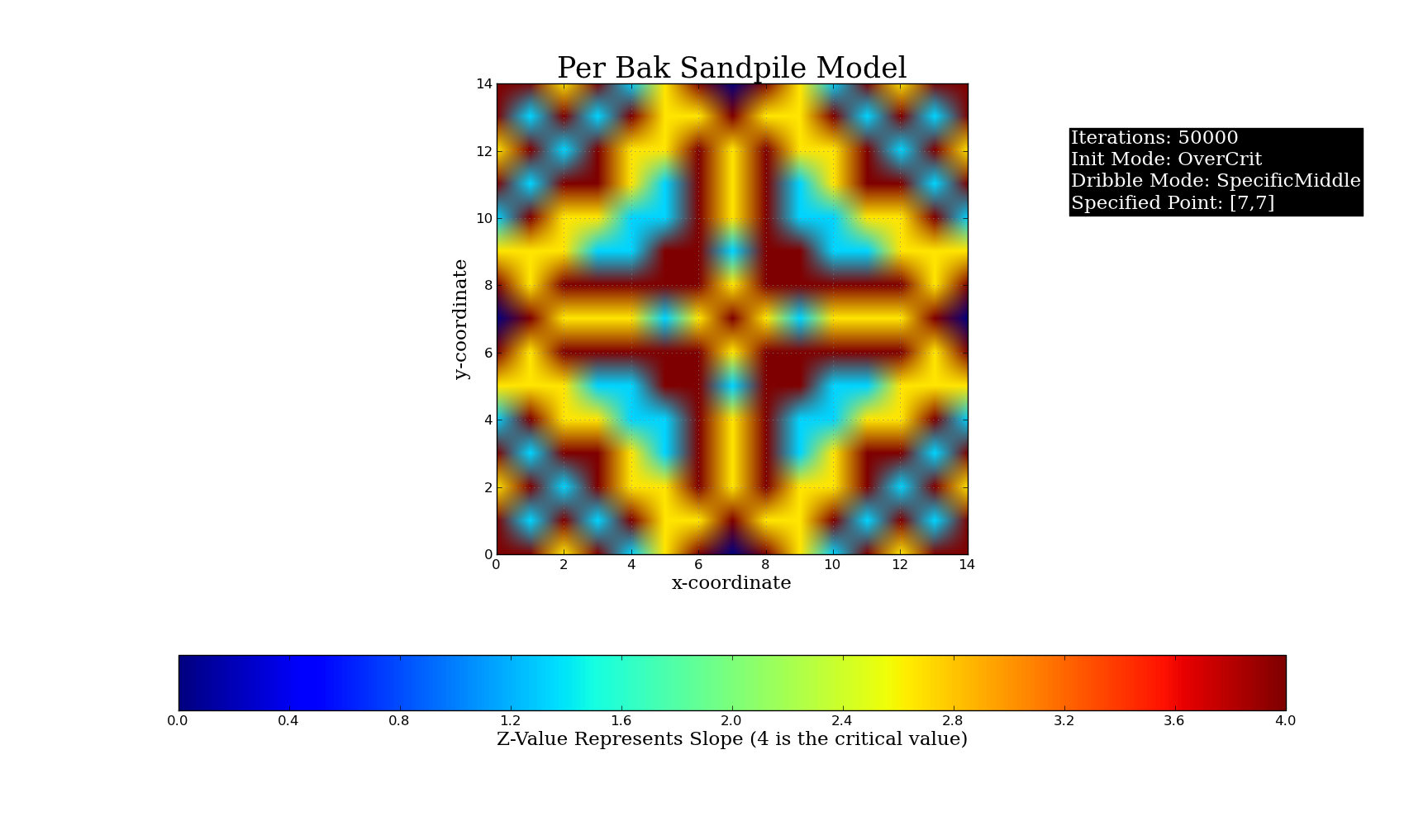
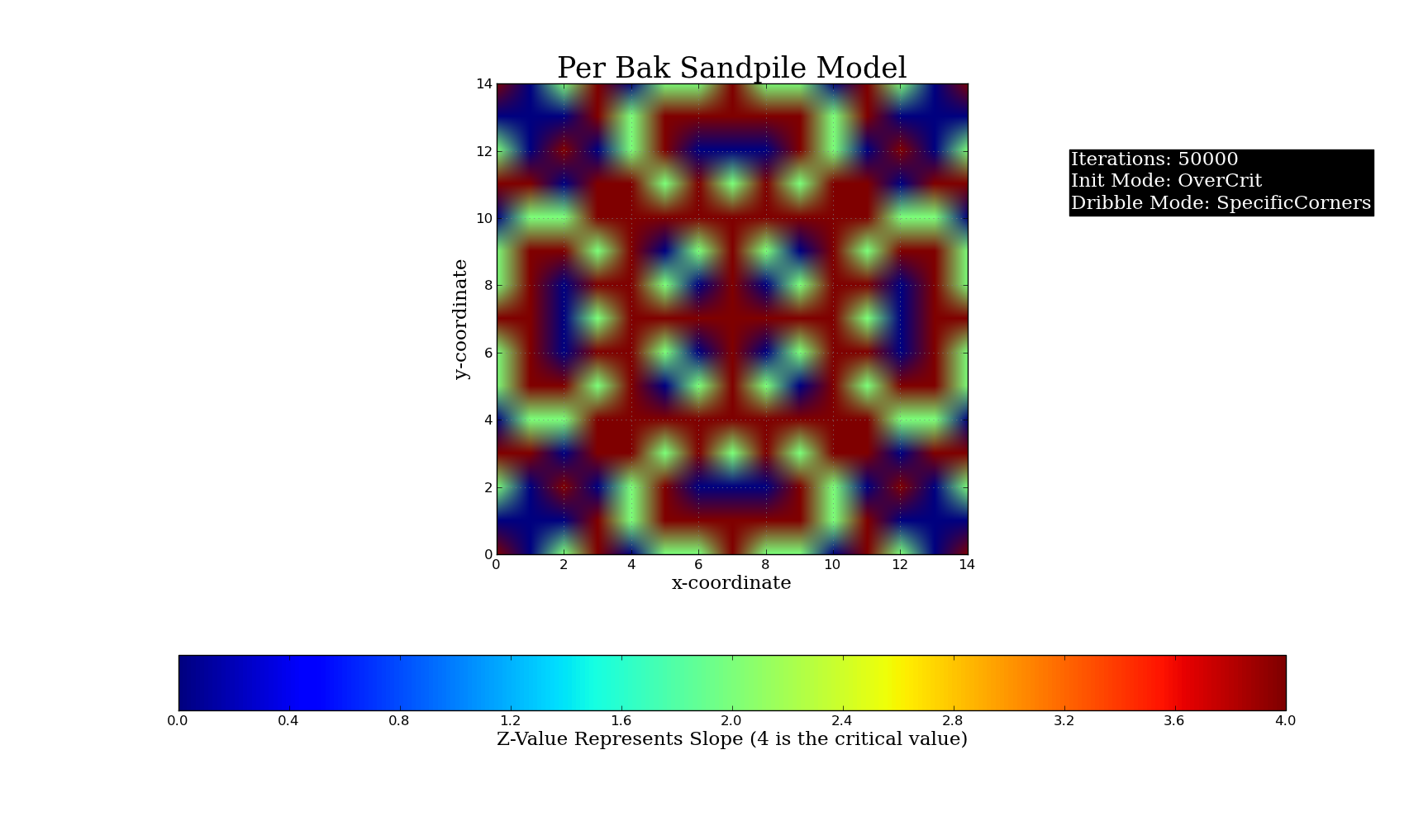
(mostly MatplotlibandNumpy). The simulation consists of a lattice of points, signified by a NxN matrix with each value in the matrix being akin to some slope value;
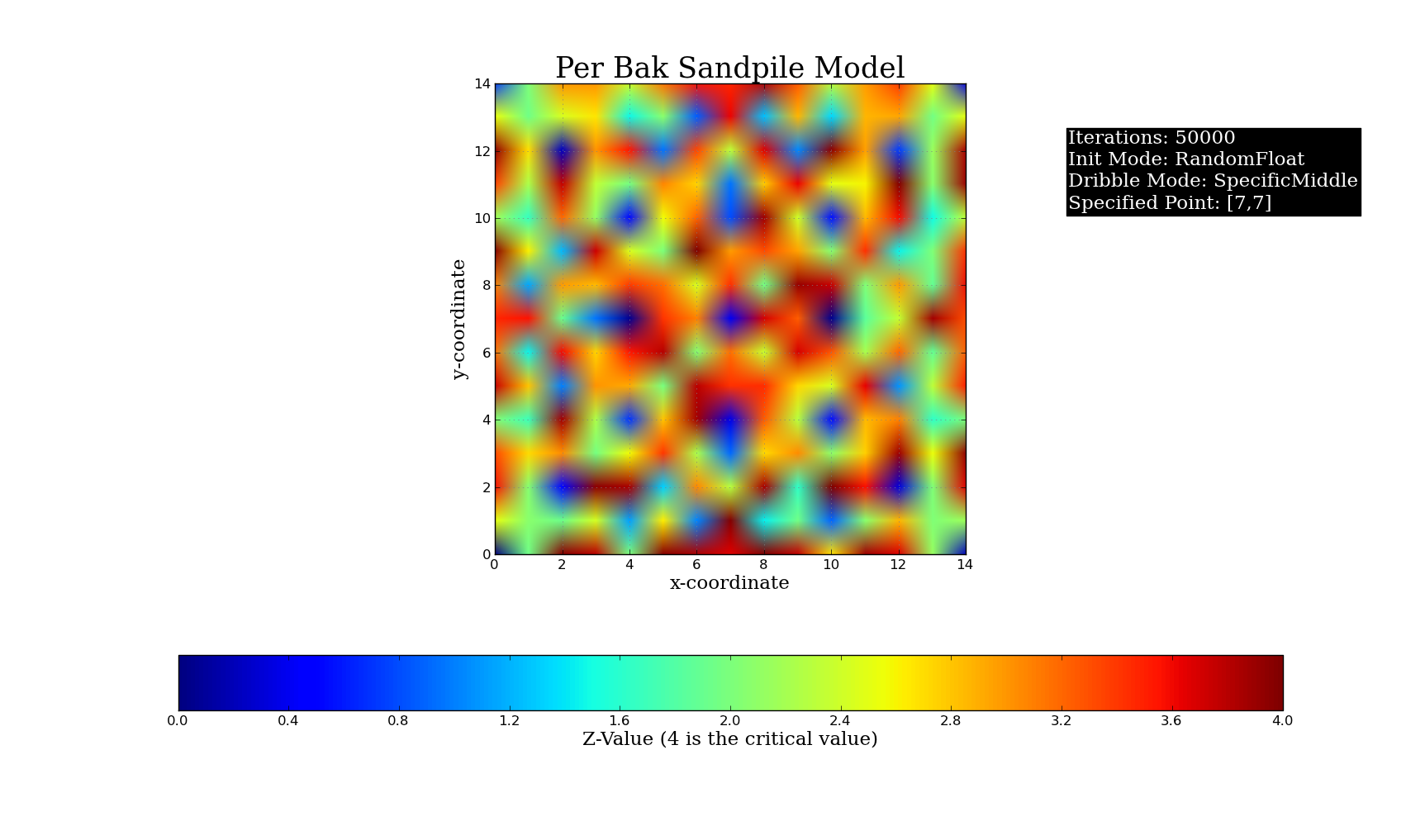
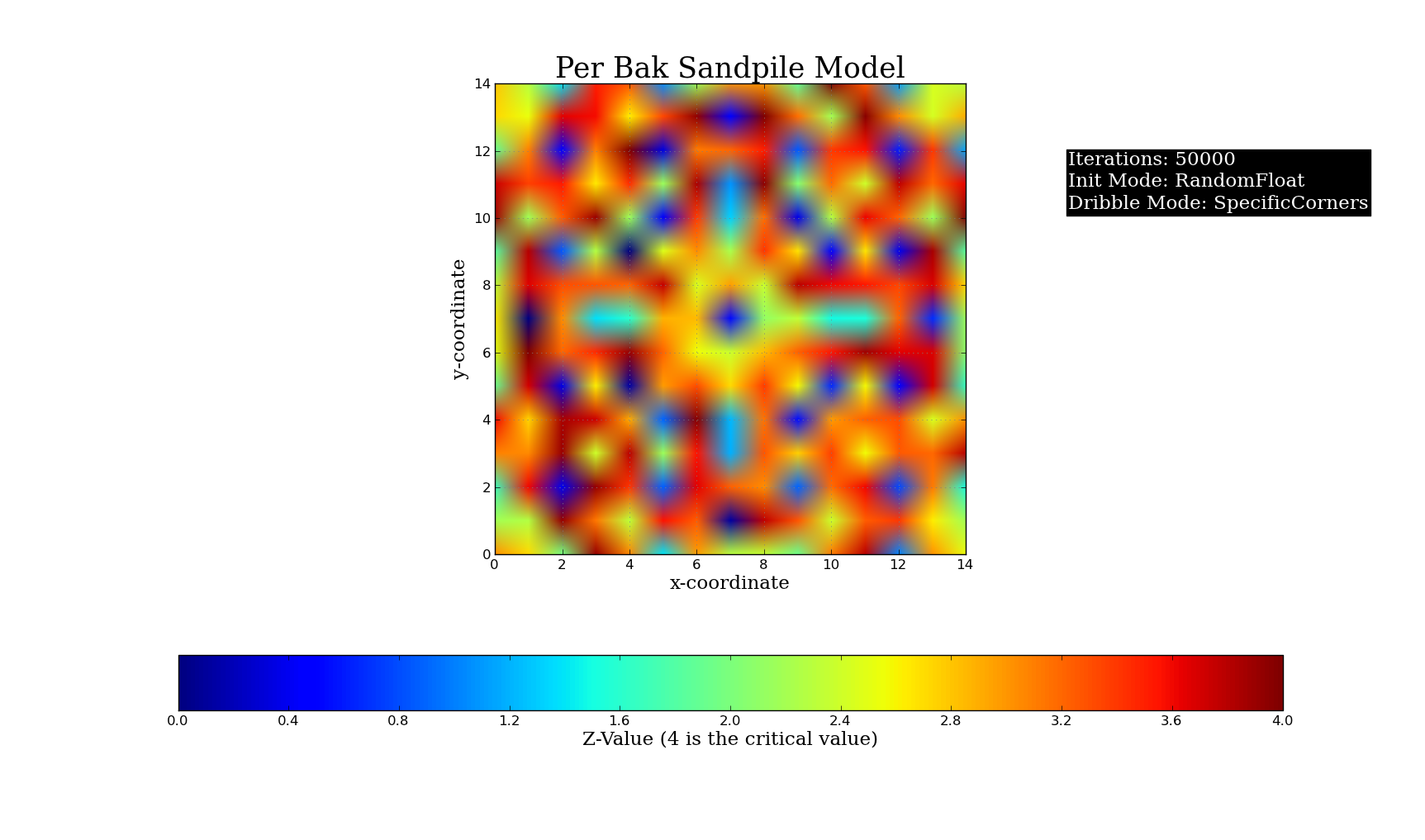
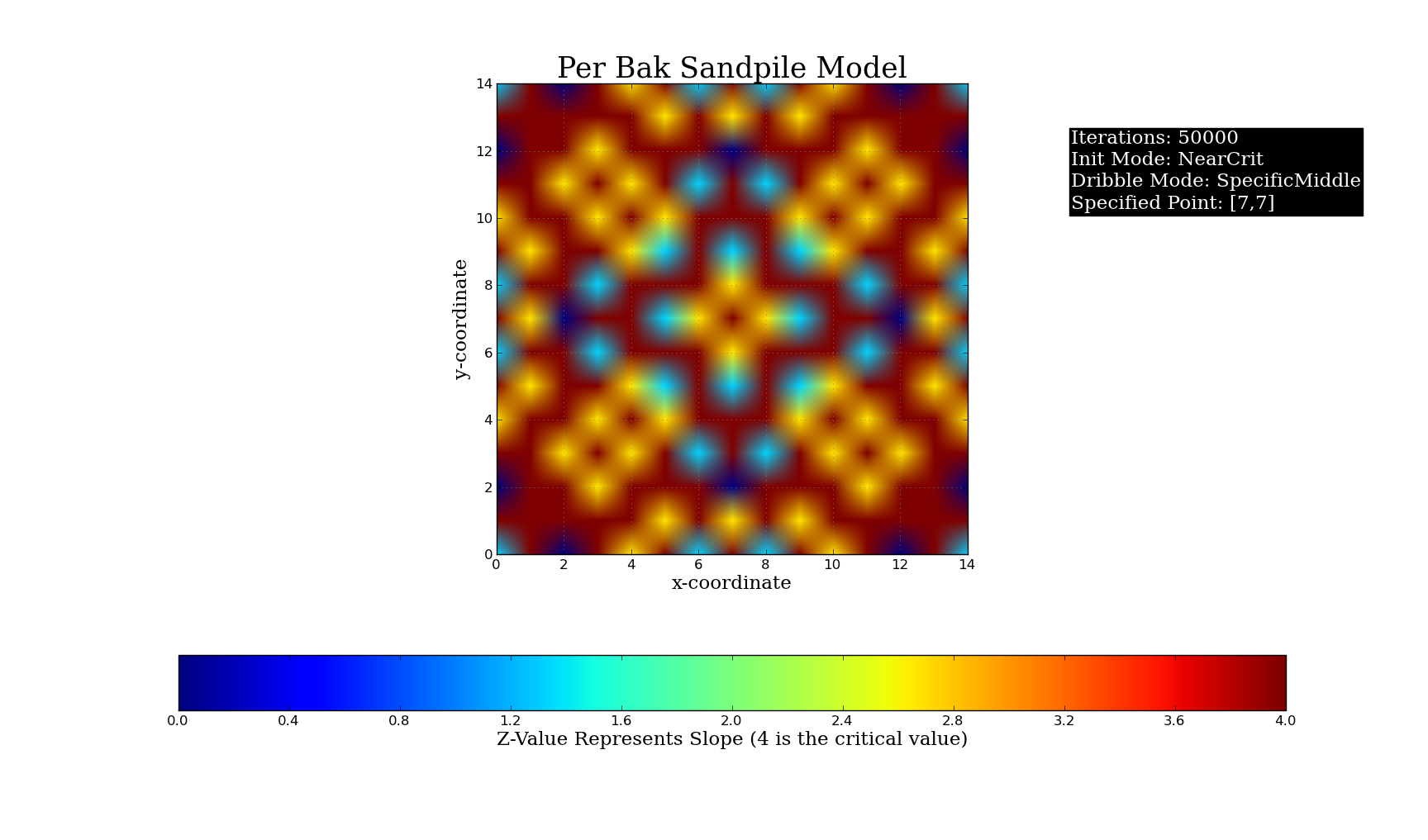
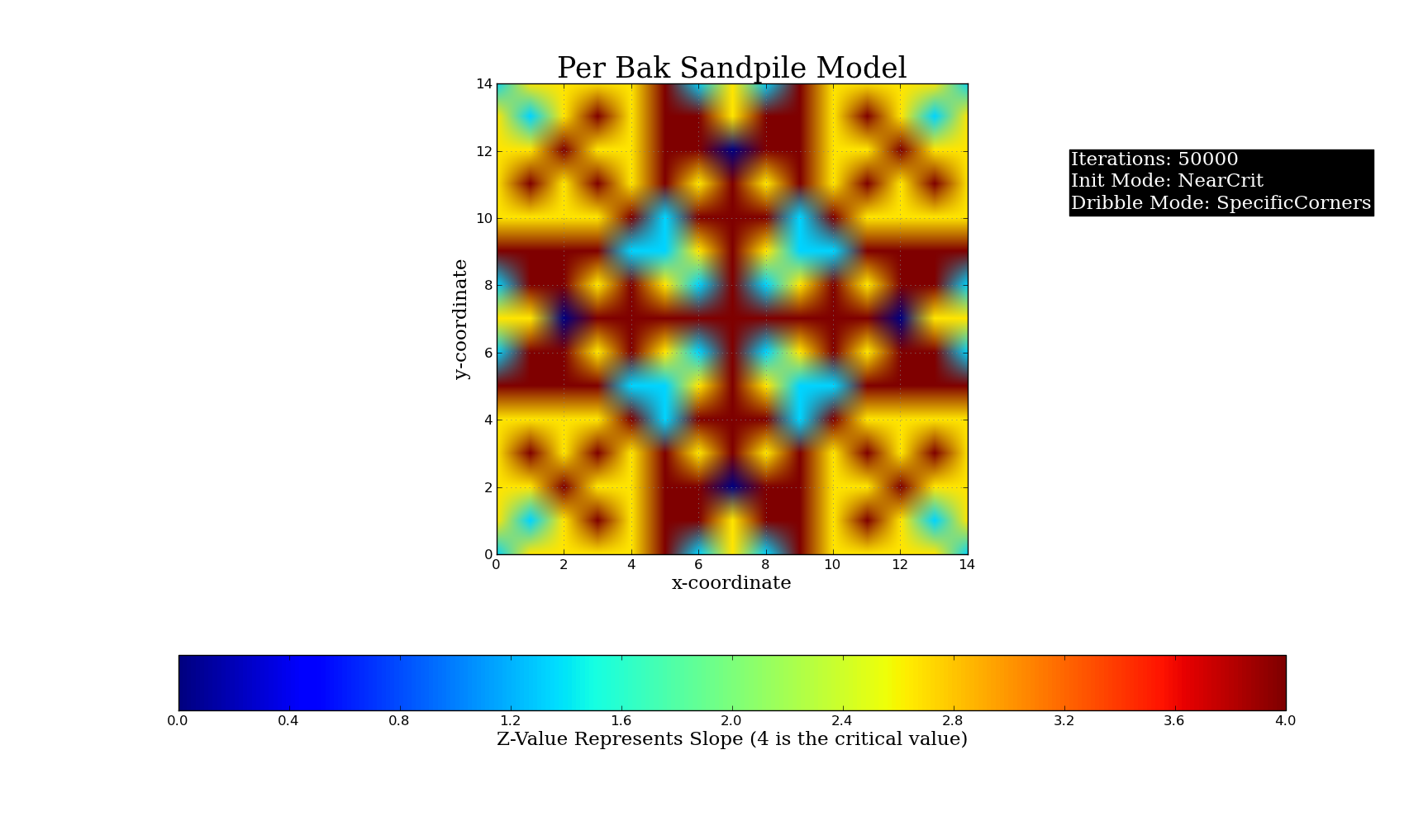
and a dribbler, which dribbles sand at some point in the lattice. The system is set up to allow random dribbling, specific centered dribbling, dribbling on a user-specified point, as well as the ability to give each point a certain slope value before starting the dribble. The user specifies a critical slope value (in my demonstration, the critical value was set to 4) and
the dribbling begins. You can specify how many iterations of dribbling to perform and save a screenshot at the end, if you like. You can also set the system to animate the dribbling, which I will demonstrate. The system will tell you how many dribbles have been performed and how many avalanches were caused by each dribble. Often, the plot will greatly change, which means that a great
number of avalanches have been caused by a dribble. I also created a Matlab demo to illustrate the differences between Python and Matlab in terms of speed and animation quality.
What did you learn from the project?
Before starting this project, I had no real knowledge of cellular automata. I had seen Conway's Game of Life and had at least a rough concept of what was happening, but I had no idea how to create my own. After reading Per Bak, I felt like I had a greater understanding of how nature works on a more detailed level. Each grain of sand when dropped has some
effect on the grains below, until the pile builds up enough to topple over or avalanche. It is so simple, yet so complex and the simulation creates a beautiful illustration of how this works.
What are you most proud of?
It took a lot of time and determination to finally understand Matplotlib enough to create an animation and save figures exactly how I wanted them. I still had some difficulties with the animations, but the end product was much smoother than my first prototype. I really liked being able to read a paper and understand it well enough mathematically to create
a working simulation with some real output. Before this class, most of my mathematical applications just spit out numbers and maybe a nice graph, but nothing was dynamic at all. Computer simulation and modeling really showed me how dynamic the biological and mechanical systems in the world are and how simple it is to model them. Although my Python implementation
is quite rudimentary, it still beautifully illustrates the fact that more catastrophes or avalanches happen on a smaller scale than on a larger scale (smaller topples happen more often than larger topples) which is what the 1/f noise would dictate.
What was your role in completing the project?
As previously mentioned, I was required to read the Physical Review Lettersjournal article and to design and implement a working simulation of the Per Bak sandpile model. I implemented the simulation in both Python and Matlab, demonstrating that Matlab is much quicker and easier to create animations and can also work with greater amounts of data (larger iterations of grains of sand dropped were
possible using Matlab). I created several animations, which I turned into youtube videos, as well as some plots to illustrate different initial condition and dribble parameters. I was required to createa presentation
to demonstrate the product to the class. I was also required to produce a formalwrite-up
displaying my knowledge of the paper I read and how my simulation demonstrated the model.
My Matlab simulations of the Bak-Tang-Wiesenfeld Sandpile Model:
Plots of Different Iteration Values (# of grains dropped) for the Matlab Simulation:
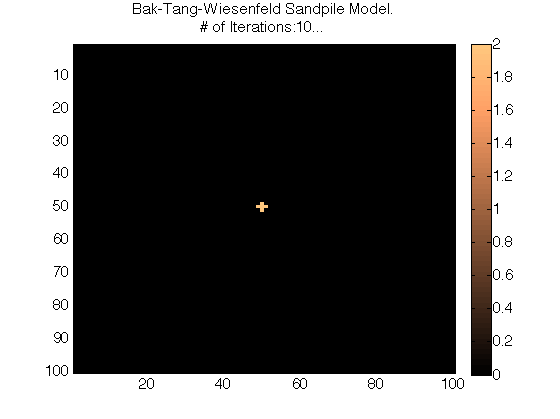
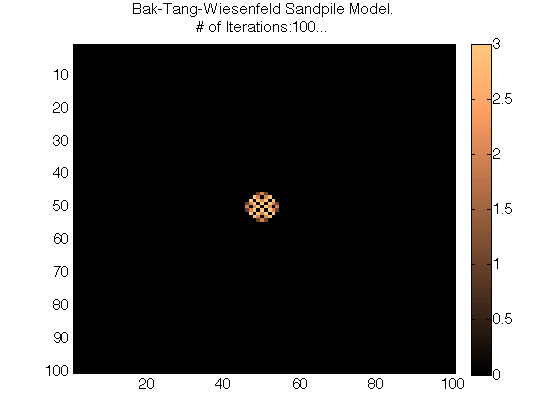
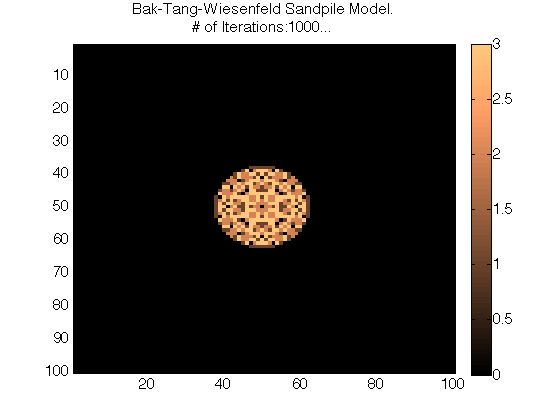
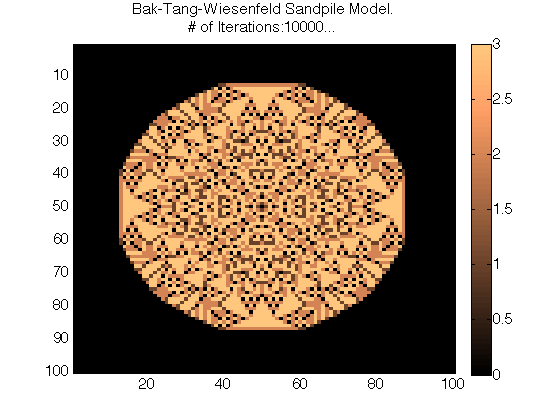
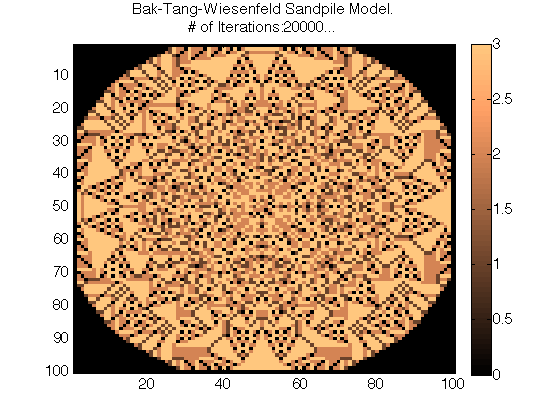
My Python Simulation of the Bak-Tang-Wiesenfeld Sandpile Model:
Plots of Different Initial Conditions for the Python Simulation (50,000 grains of sand, Critical Value = 4):
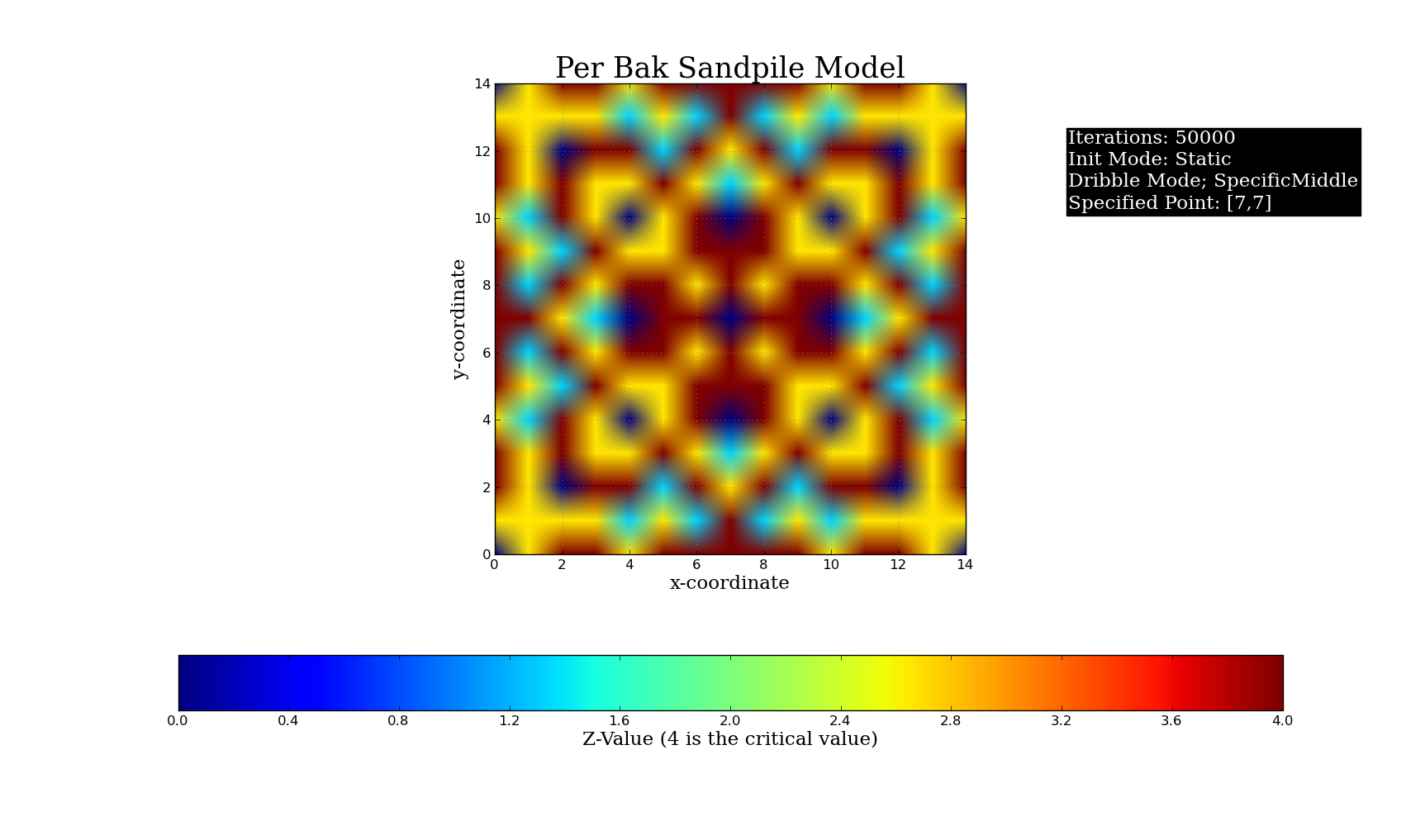
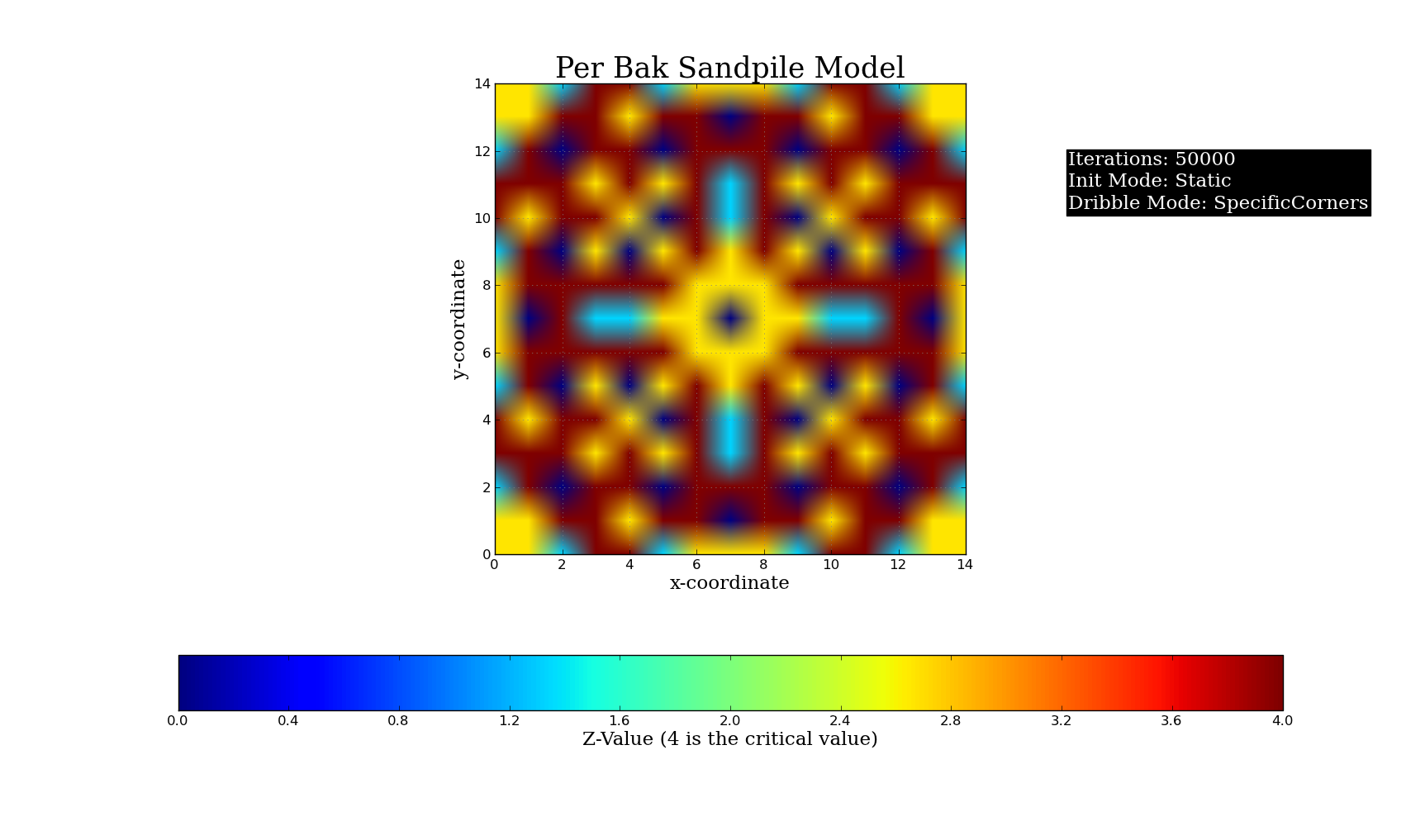
What would you do differently next time?
If I had my choice, I would use Matlab for this simulation. I also would've liked to have time to create a 3D version of this simulation to be
able to see the individual sandpiles form. As shown in my examples of Cellular Automata written in Matlab, there is a lot of power in Matlab that
can be harnessed for this type of project. I really have a love for Python when it comes to a lot of things, but I haven't mastered the animations
of Matplotlib plots yet. I think a future project is in store for me to learn more about Python animations!
This project is also found onGitHub